随着一声震动,你的手机收到了一条消息。你迫不及待地拿起手机,手机内置的机器学习算法识别了你的脸,判断你就是你本人,并为你进行了解锁。
早已习惯这一切的你甚至忘记了这一过程,直到戴着口罩的你不得不手动输入数字密码,或者为了解锁暂时拉下口罩。
随着机器学习持续不断的火热,我们生活中的方方面面都早已有了它的影子。你感叹围棋和游戏的AI战胜了顶尖的人类,也会因为抖音和淘宝比你自己更了解你而感到惊悚。
你习惯了美颜相机可以精准地找到你的脸,也期盼着能坐上会自动驾驶的汽车。
但在这个人人大谈特谈大数据、人工智能、机器学习的时代,你是否知道它们到底什么?学过一点代码的你是不是也很想亲手体验一下训练一个自己的AI呢?
下面我们将通过讲解一个经典入门例子,带你一步一步训练一个简单的神经网络。
什么是机器学习?
机器学习,顾名思义就是让机器来学习。学习我们再熟悉不过了,但让机器学习是什么意思?难道这些芯片有了智慧?
现实并没有那么玄乎,现在的人工智能技术还远远没有达到那样的高度,我们能做的只是让算法根据经验来做出判断。用我们专业的学习术语来讲,就是背答案。
人类学习的时候,会有学习资料和考试,我们把学习资料称为训练集(training set),考试试卷称为测试集(testing set),它们统称数据集。
所以机器学习的过程就是让我们的模型把训练集的资料背下来,然后在测试集的考试中考个高分,这个模型就训练完成,可以走向工作岗位了。
等等,模型是什么?它可以是一个传统的数学概率模型,也可以是一个现在大火的神经网络。
我们给机器做的任务一般比较简单,并且有某些隐秘的规律可循,比如识别一个图片中的物体,或者在人海之中找到一个人,又或者判断一个音乐或句子的情感,也可能是预测明天的股票趋势。
这些问题一般都是分类问题或者回归问题。
这篇文章将要介绍的,就是一个用于图片分类的神经网络模型。我们的目标是判断一个手写数字到底是几,这就是大名鼎鼎的Yann Lecun的MNIST数据集。

如何分类?
(如果你想跳过原理直接看代码,可以跳过这两章)
分类问题通俗地讲就是把一个集合里的元素根据他们的特性打上标签。比如把一个文件夹中的宠物图片分成猫和狗,或者判断一张图片是猫还是狗,二者是同一个问题。

这里我们举一个传统的机器学习例子,把二维平面上的点分类。平面中有一些点,它们有坐标和颜色。我们有一个新的点,想根据新的点的坐标来预测它是什么颜色。
最简单的方法是画一条线,图中的直线都可以很好地将平面划分成两部分,将已有的数据完美分类。所以图中的任意一条线都可以是我们想要的模型。
但是,如果样本的分布没有这么规律,我们不能用一条直线甚至不能只用一条曲线来分割它们怎么办?况且这只是一个二维模型,如果我们有更多维度的数据、甚至是一张1080p的图片那么大,我们该怎么办?
传统方法自有它的解决办法,但我们要讲的是神经网络的办法。
首先从上面的例子我们知道了数据的基本样子:一个坐标和一个标签。这个坐标可能远不止二维,甚至可能包含了图片中每个像素点的RGB值。这个标签就是我们要预测的“答案”。
那么怎么把图片中那么多数据总结为一个值呢?这就需要用到神经元网络的连接了。神经网络(或者叫人工神经元网络 Artificial Neural Network、多层感知器 Multilayer Perceptron)由一个个神经元组成,我们先来看一个神经元是什么。
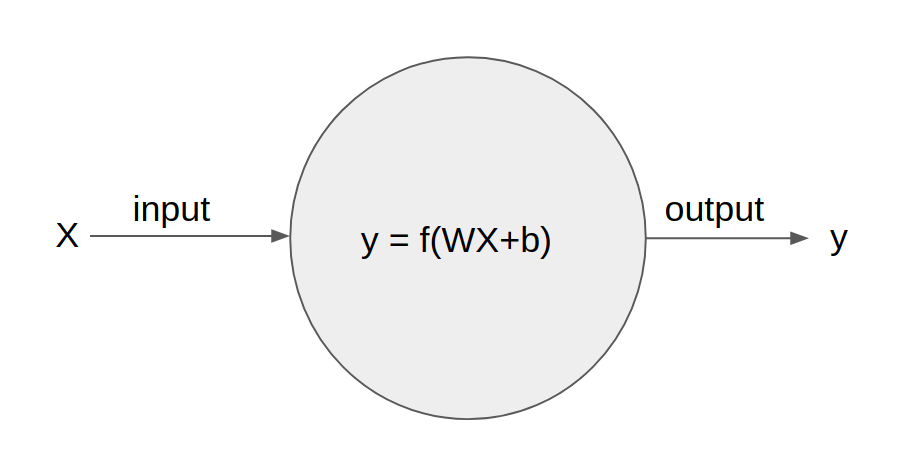
这就是神经网络里一个普普通通的神经元了。它代表了一次计算,它有输入向量X和输出y,并且内部存有权重(weight)向量W和偏置(bias) b,还有激活函数(activation function)f。
先不要急着头疼,这只涉及简单的数学知识。你并不需要理解它,也可以制作自己的神经网络,你只需要知道它是最基本的单位,并且在之后用它来组装就可以了。
首先这个神经元会计算W*X + b的值,其中W和X是相同维度的向量(vector),我们计算它们的内积(product),也就是w1x1+w2x2+w3x3+…
至于为什么我们会把输入写成向量,那就是因为这个神经元前面可能会连接多个神经元作为输入,所以我们把这些输入放在一起写作向量X,就是这么简单。
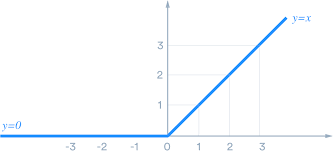
那我们为什么需要激活函数f呢?因为试想我们如果把不加f的一串神经元连起来,那最后的结果就还会是一个线性变换,在二维的例子中我们不希望用一条直线来分割样本,同理在高维度中我们不希望用超平面来做分类,所以我们可以用类似下面这样的一个函数(图中是ReLU函数)来强行把结果变成非线性。到现在为止这些计算听起来十分荒诞,但我们就是在模拟生物中一个神经元的工作方式:接受刺激,然后做出或不做出反应。
那么我们怎么知道W和b都是多少呢?这就需要训练了,在一个有成千上万神经元的网络里,我们不可能手动地设置每一个权重。我们可以求出y和真正答案的差值,称为损失loss。然后通过逆向求偏导,把X当成常数,而把W和b当成变量,我们就知道为了得到正确答案,W和b应该如何修改了。这在神经网里称为反向传播(backpropagation)。所以假如我们有一个神经元,我们想要训练它,就不断地把样本一个一个地输进去,进行正向和逆向传播,让它一点一点自动逐渐修改W和b的值,直到我们满意为止。这个过程就叫随机梯度下降(Stochastic gradient descent, SGD)。
一个神经元能做的事是远远不够的,所以我们将大量神经元连在一起,连接输入变量的叫做输入层(input layer),连接输出的叫输出层(output layer),中间的叫做隐层(hidden layer)。
输入层的神经元数量等于输入的维度,输出层神经元的数量等于我们要分的类数,这样输出层的哪个神经元输出的值最高,我们就判定样本属于哪一类。
为了让模型产生足够复杂的变化,隐层自然是越多越好。但相对地,隐层越多,计算量和训练所需样本就越多。在网络中我们可以根据链式法则求偏导,所以最终的loss会一路从最后一层反向传播回第一层。
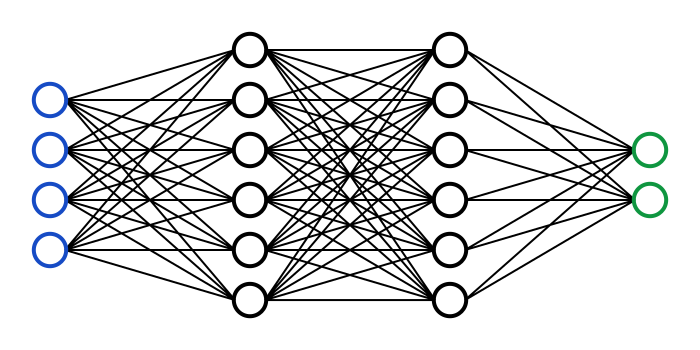
这样,一个简单的全连接(fully connected)神经网就建好了。全连接顾名思义就是把相邻两层的神经元能连的都连上了。这在低维数据上可以彻底利用所有输入之间隐秘的关系,但在像图片这么大的数据上,就会有很多连接,并且做了很多没用的计算,使得训练变得很慢而且低效。比如,图片的左上角和右下角往往没什么关系,那么我们就不需要讲这两部分的输入连接到同一个神经元上。
事实上人也不是这样看图的,如果人要判断一张图片是猫,那么可能我们的大脑会先判断图中有眼睛鼻子嘴巴耳朵,然后这些器官组成了一只猫的脸,而不是根据一整张图的每个点一起判断的。所以在图片分类中,我们会用卷积神经网(convolutional neural network)来节约计算。
卷积神经网
这个名字听起来很玄乎,但其实道理很简单:图片是二维的,那么我们就用一个很小的二维神经层来扫描这张图,一遍扫一边计算输出,扫过一遍之后,它们的输出就又拼成了一张图。
这就好像是拿着放大镜看报纸,放大镜相比于报纸很小,但扫过一遍之后却能得到一整张报纸的图像。

这个二维神经元层我们称作kernel,所做的计算就称为卷积。
我们把几个kernel放在一起,作为卷积神经网中的一个卷积层(conv layer)。每个kernel用来检测某种特定的特征(feature)。我们创建的时候并不知道它们会检测什么特征,一切都靠机器自己学习。
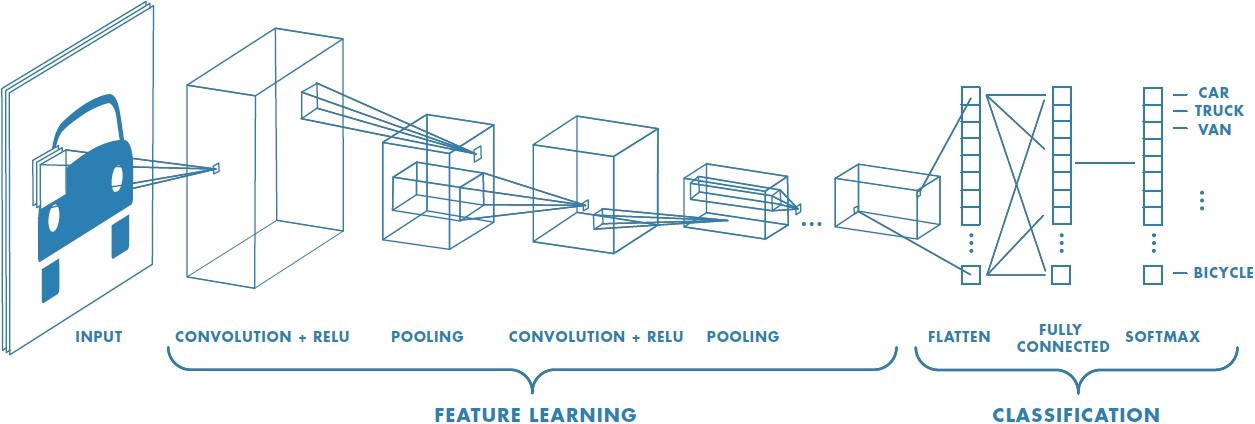
然后我们再把这层的输出缩小(pooling layer),然后用下一层的kernel继续扫描,直到得到的输出图足够小了,我们再把每个像素点连起来,构成全连接输出层。这就形成了下面这样的卷积神经网。
代码环节
下面我们开始实战!首先确保你有一台电脑,它不必有GPU,这个简单的模型用CPU运算已经足够。
本篇文章我们采用linux系统演示,mac和windows除了环境配置不同以外,其他的代码都相同。
首先确保你有python3(建议使用Anaconda),然后我们来用这个网页中的命令安装深度学习框架pytorch。如果没有安装anaconda请选择Pip。
https://pytorch.org/get-started/locally/
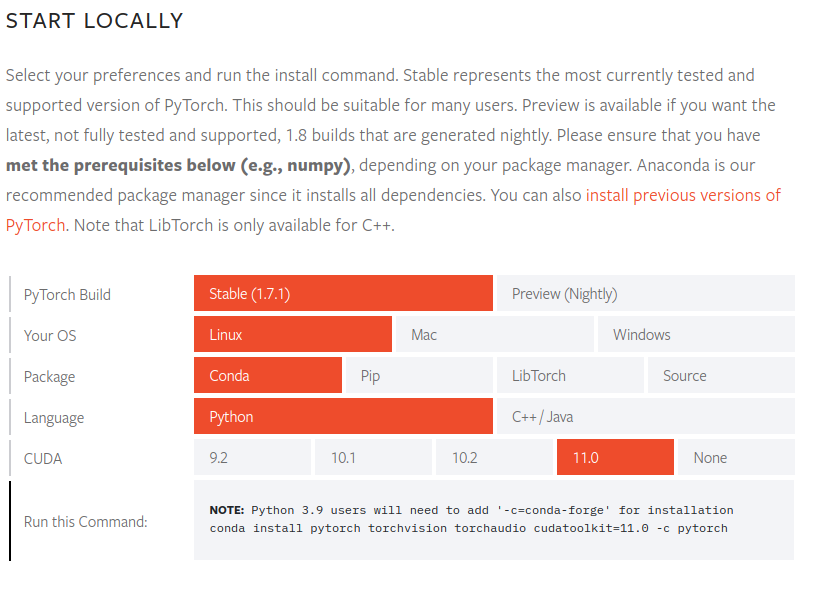
然后创建一个”mnist.py”,我们就可以写(抄)代码啦。本代码抄自我非常敬佩的NYU教授Alfredo的教程(https://github.com/Atcold/pytorch-Deep-Learning/blob/master/06-convnet.ipynb)。
首先引入必要的库,如果没有其中的库请自行搜索如何安装
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")然后下载mnist数据集并做一些变换处理
input_size = 28*28 # images are 28x28 pixels
output_size = 10 # there are 10 classes
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=1000, shuffle=True)然后我们可以看一看数据的样子
plt.figure(figsize=(16, 6))
for i in range(10):
plt.subplot(2, 5, i + 1)
image, _ = train_loader.dataset.__getitem__(i)
plt.imshow(image.squeeze().numpy())
plt.axis('off')
plt.show()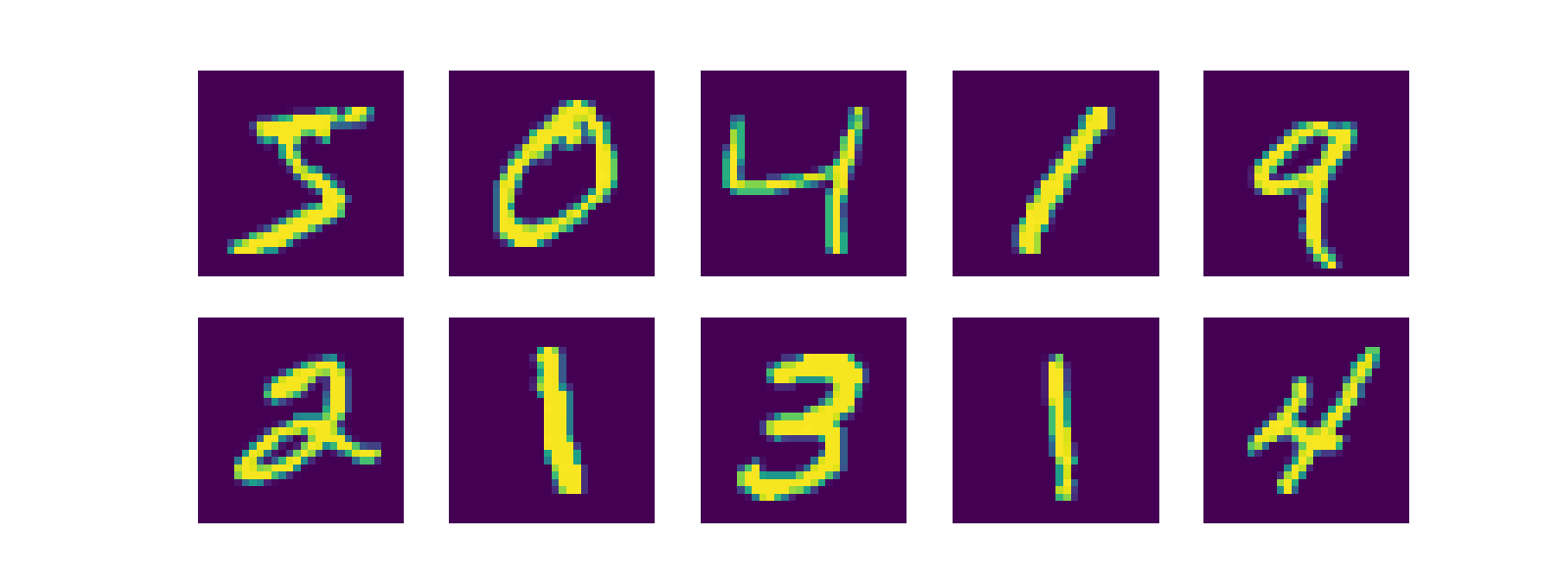
接下来定义全连接和卷积神经网两种模型,我们后面可以比较这两种模型的准确度。
class FC2Layer(nn.Module):
def __init__(self, input_size, n_hidden, output_size):
super(FC2Layer, self).__init__()
self.input_size = input_size
self.network = nn.Sequential(
nn.Linear(input_size, n_hidden), # 一层全连接
nn.ReLU(), # 一层激活
nn.Linear(n_hidden, n_hidden), # 又一层全连接
nn.ReLU(), # 又一层激活
nn.Linear(n_hidden, output_size), # 最后一层全连接
nn.LogSoftmax(dim=1) # 用来使结果更明显
)
def forward(self, x):
x = x.view(-1, self.input_size)
return self.network(x)
class CNN(nn.Module):
def __init__(self, input_size, n_feature, output_size):
super(CNN, self).__init__()
self.n_feature = n_feature
self.conv1 = nn.Conv2d(
in_channels=1, out_channels=n_feature, kernel_size=5)
self.conv2 = nn.Conv2d(n_feature, n_feature, kernel_size=5)
self.fc1 = nn.Linear(n_feature*4*4, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x, verbose=False):
x = self.conv1(x) # 一层卷积
x = F.relu(x) # 一层激活
x = F.max_pool2d(x, kernel_size=2) # 一层池化,用来缩小
x = self.conv2(x) # 第二层卷积
x = F.relu(x) # 第二层激活
x = F.max_pool2d(x, kernel_size=2) # 第二层池化
x = x.view(-1, self.n_feature*4*4) # 转为一维
x = self.fc1(x) # 全连接
x = F.relu(x) # 激活
x = self.fc2(x) # 全连接
x = F.log_softmax(x, dim=1) # logsoftmax
return x现在我们就定义了一个全连接的模型和一个简化版的LeNet(LeNet见下图)
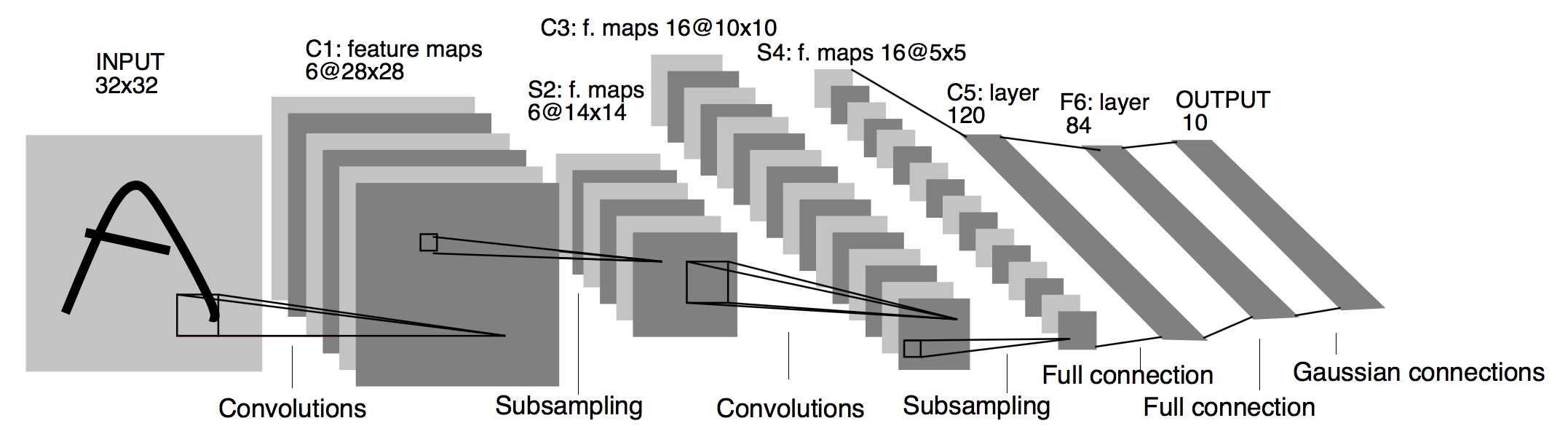
然后我们定义train和test函数,用它们进行计算
def train(epoch, model, perm=torch.arange(0, 784).long()):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
# send to device
data, target = data.to(device), target.to(device)
# permute pixels
data = data.view(-1, 28*28)
data = data[:, perm]
data = data.view(-1, 1, 28, 28)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test(model, perm=torch.arange(0, 784).long()):
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
# send to device
data, target = data.to(device), target.to(device)
# permute pixels
data = data.view(-1, 28*28)
data = data[:, perm]
data = data.view(-1, 1, 28, 28)
output = model(data)
# sum up batch loss
test_loss += F.nll_loss(output, target, reduction='sum').item()
# get the index of the max log-probability
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).cpu().sum().item()
test_loss /= len(test_loader.dataset)
accuracy = 100. * correct / len(test_loader.dataset)
accuracy_list.append(accuracy)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
accuracy))然后开始训练FNN!
n_hidden = 8 # number of hidden units
model_fnn = FC2Layer(input_size, n_hidden, output_size)
model_fnn.to(device)
optimizer = optim.SGD(model_fnn.parameters(), lr=0.01, momentum=0.5)
for epoch in range(0, 1):
train(epoch, model_fnn)
test(model_fnn)会生成这样的结果,说明我们的准确率有89%,还不错
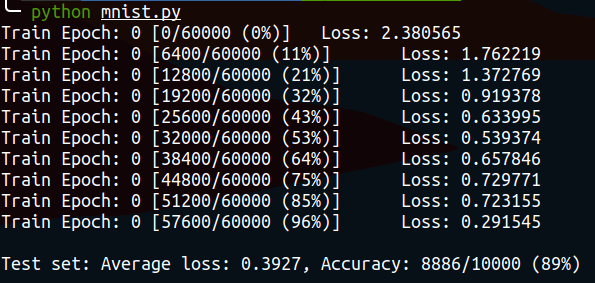
再来试试CNN!
n_features = 6 # number of feature maps
model_cnn = CNN(input_size, n_features, output_size)
model_cnn.to(device)
optimizer = optim.SGD(model_cnn.parameters(), lr=0.01, momentum=0.5)
for epoch in range(0, 1):
train(epoch, model_cnn)
test(model_cnn)结果如下,可以看到测试集上的准确率明显提高了。
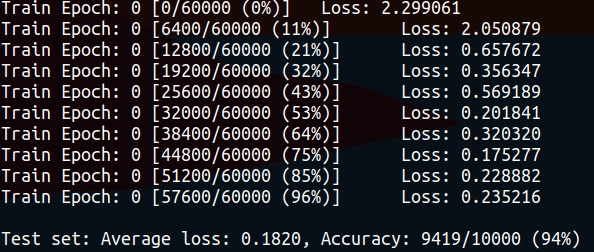
感兴趣的同学可以尝试修改层数、特征数、learning rate等各种参数,甚至修改预处理的方式,来探索会有什么不同。也可以尝试把epoch调高,看看训练更长时间loss的收敛情况。
P.S. 文中代码可以点击这里下载哦!